
3.8 Application of the Momentum Equation
example 1:
The figure below shows a smooth curved vane attached to a rigid foundation. The jet of water, rectangular in section, 75mm wide and 25mm thick, strike the vane with a velocity of 25m/s. Calculate the vertical and horizontal components of the force exerted on the vane and indicate in which direction these components act.
[Horizontal 233.4 N acting from right to left. Vertical 1324.6 N acting downwards]
From the question:
Calculate the total force using the momentum equation:
Body force and pressure force are 0.
So force on vane:
example 2:
A 600mm diameter pipeline carries water under a head of 30m with a velocity of 3m/s. This water main is fitted with a horizontal bend which turns the axis of the pipeline through 75 (i.e. the internal angle at the bend is 105). Calculate the resultant force on the bend and its angle to the horizontal.
[104.044 kN, 52 29']
A 600mm diameter pipeline carries water under a head of 30m with a velocity of 3m/s. This water main is fitted with a horizontal bend which turns the axis of the pipeline through 75 (i.e. the internal angle at the bend is 105). Calculate the resultant force on the bend and its angle to the horizontal.
[104.044 kN, 52 29']
From the question:
Calculate total force.
Calculate the pressure force
p1 = p2 = p = hrg = 3010009.81 =
294.3 kN/m2
There is no body force in the x or y directions.
These forces act on the fluid
The resultant force on the fluid is
example 3:
A horizontal jet of water 2103 mm2 cross-section and flowing at a velocity of 15 m/s hits a flat plate at 60 to the axis (of the jet) and to the horizontal. The jet is such that there is no side spread. If the plate is stationary, calculate a) the force exerted on the plate in the direction of the jet and b) the ratio between the quantity of fluid that is deflected upwards and that downwards. (Assume that there is no friction and therefore no shear force.)
[338N, 3:1]
From the question a2 = a3 =2x10-3 m2
u = 15 m/s
Apply Bernoulli,
Change in height is negligible so z1 = z2 = z3
and pressure is always atmospheric p1= p2 = p3
=0. So
u1= u2 = u3 =15 m/s
By continuity Q1= Q2 + Q3
u1a1 = u2a2 + u3a3
so a1 = a2 + a3
Put the axes normal to the plate, as we know that the resultant force is
normal to the plate.
Q1 = a1u = 210-315 = 0.03
Q1 = (a2 + a3) u
Q2 = a2u
Q3 = (a1 - a2)u
Calculate total force.
Component in direction of jet = 390 sin 60 = 338 N
As there is no force parallel to the plate Fty = 0
Thus 3/4 of the jet goes up, 1/4 down
example 4:
A 75mm diameter jet of water having a velocity of 25m/s strikes a flat plate, the normal of which is inclined at 30 to the jet. Find the force normal to the surface of the plate.
[2.39kN]
From the question, djet = 0.075m u1=25m/s
Q = 25p(0.075/2)2 = 0.11 m3/s
Force normal to plate is
FTx = rQ( 0 - u1x )
FTx = 10000.11 ( 0 - 25 cos 30 ) = 2.39 kN
example 5:
The outlet pipe from a pump is a bend of 45 rising in the vertical plane (i.e.
and internal angle of 135). The bend is 150mm diameter at its inlet and 300mm
diameter at its outlet. The pipe axis at the inlet is horizontal and at the
outlet it is 1m higher. By neglecting friction, calculate the force and its direction
if the inlet pressure is 100kN/m2 and the flow of water through the
pipe is 0.3m3/s. The volume of the pipe is 0.075m3.
[13.94kN at 67 40' to the horizontal]
[13.94kN at 67 40' to the horizontal]
1&2 Draw the control volume and the axis system
p1 = 100 kN/m2, Q = 0.3 m3/s q = 45
d1 = 0.15 m d2 = 0.3 m
A1 = 0.177 m2 A2 = 0.0707 m2
3 Calculate the total force
in the x direction
and in the y-direction
4 Calculate the pressure force.
We know pressure at the inlet but not at the outlet.
we can use Bernoulli to calculate this unknown pressure.
where hf is the friction loss
In the question it says this can be ignored, hf=0
The height of the pipe at the outlet is 1m above the inlet.
Taking the inlet level as the datum:
z1 = 0 z2 = 1m
So the Bernoulli equation becomes:
5 Calculate the body force
The only body force is the force due to gravity. That is the weight
acting in the y direction.
There are no body forces in the x direction,
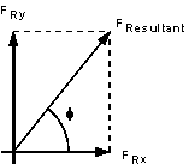
6 Calculate the resultant force
And the resultant force on the fluid is given by
And the direction of application is
The force on the bend is the same magnitude but in the opposite
direction
example 6:
The force exerted by a 25mm diameter jet against a flat plate normal to the axis of the jet is 650N. What is the flow in m3/s?
[0.018 m3/s]
From the question, djet = 0.025m FTx = 650 N
Force normal to plate is
FTx = rQ( 0 - u1x )
650 = 1000Q ( 0 - u )
Q = au = (pd2/4)u
650 = -1000au2 = -1000Q2/a
650 = -1000Q2/(p0.0252/4)
Q = 0.018m3/s
example 7:
A curved plate deflects a 75mm diameter jet through an angle of 45. For a velocity in the jet of 40m/s to the right, compute the components of the force developed against the curved plate. (Assume no friction).
[Rx=2070N, Ry=5000N down]
From the question:
Calculate the total force using the momentum equation:
Body force and pressure force are 0.
So force on vane:
example 8:
A 45 reducing bend, 0.6m diameter upstream, 0.3m diameter downstream, has water flowing through it at the rate of 0.45m3/s under a pressure of 1.45 bar. Neglecting any loss is head for friction, calculate the force exerted by the water on the bend, and its direction of application.
[R=34400N to the right and down, q = 14]
1&2 Draw the control volume and the axis system
p1 = 1.45105 N/m2, Q = 0.45 m3/s
q = 45
d1 = 0.6 m d2 = 0.3 m
A1 = 0.283 m2 A2 = 0.0707 m2
3 Calculate the total force
in the x direction
and in the y-direction
4 Calculate the pressure force.
We know pressure at the inlet but not at the outlet.
we can use Bernoulli to calculate this unknown pressure.
where hf is the friction loss
In the question it says this can be ignored, hf=0
Assume the pipe to be horizontal
z1 = z2
So the Bernoulli equation becomes:
5 Calculate the body force
The only body force is the force due to gravity.
There are no body forces in the x or y directions,
6 Calculate the resultant force
And the resultant force on the fluid is given by
And the direction of application is
The force on the bend is the same magnitude but in the opposite
direction











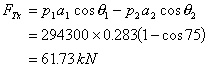








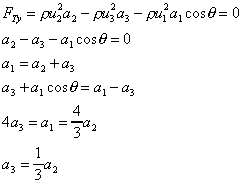








































very nice and the cctv there was very funny to me
ReplyDelete